Fixed-point Convolution Framework
Introduction
We propose a fixed-point convolution strategy based on the distribution characteristics of activation values. We first propose to perform the activation range pre-processing by constraining its dynamic range into a limited scope, of which we re-train the original floating-point model till the convergence with decent trade-off balance. Upon this re-trained floating-point model with limited activation range, we have then developed the range-adaptive quantization, linear scaling, and range-dependent normalization to replace the default floating-point weights, biases, and activations involved in native floating-point convolutions, and exponential computations (e.g.,sigmoid, softmax-based normalization), into the fixed-point presentation. The “range” used here can be represented by a scalar that is fixed for pre-processing, learned for quantization, and adapted for normalization, in neural model for indicating the dynamic range of the processing data for compact data presentation. Since floating-point operations are not involved in the forward inference process, but only fixed-point operations with low bit-width are involved, the instability of floating-point operations on different hardware architectures can be avoided, and calculations can also be accelerated.
Architecture
After the floating-point convolution kernel is decomposed into a same-size integer convolution kernel and a fixed-point range parameter, the original floating-point convolution layer is divided into two layers: the first layer is a similar fixed-point convolution layer, and the second layer is a linear scaling layer.
The following figure shows the process of decomposing the floating-point convolution kernel into integer convolution kernels and range parameters:

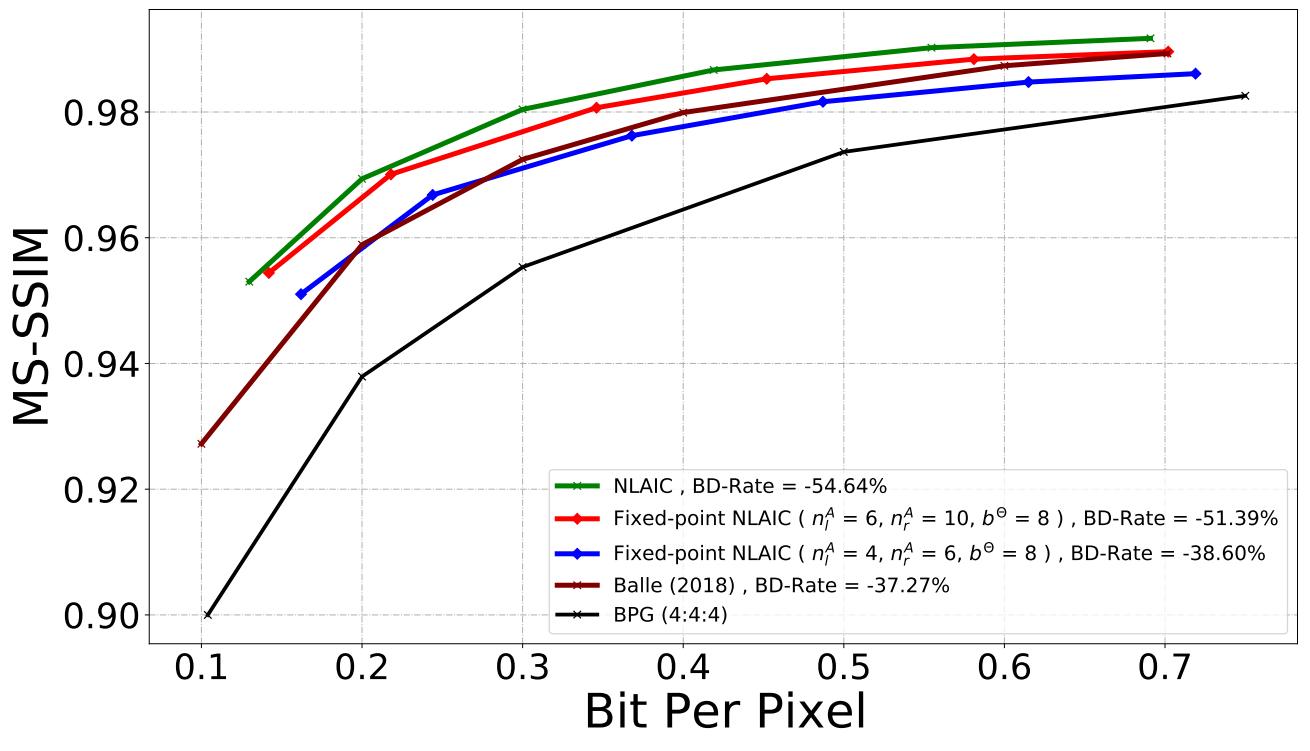
Rate-Distortion Performance (MS-SSIM & PSNR)
Pre-processing
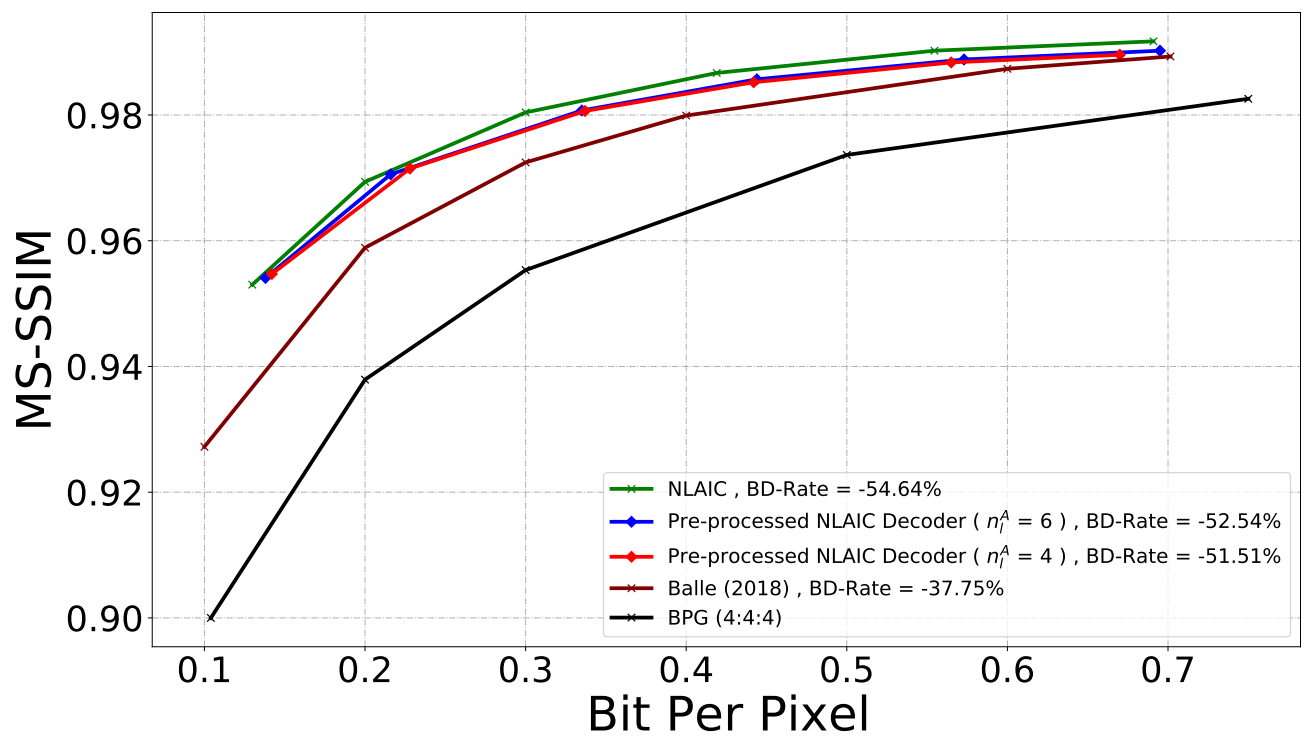
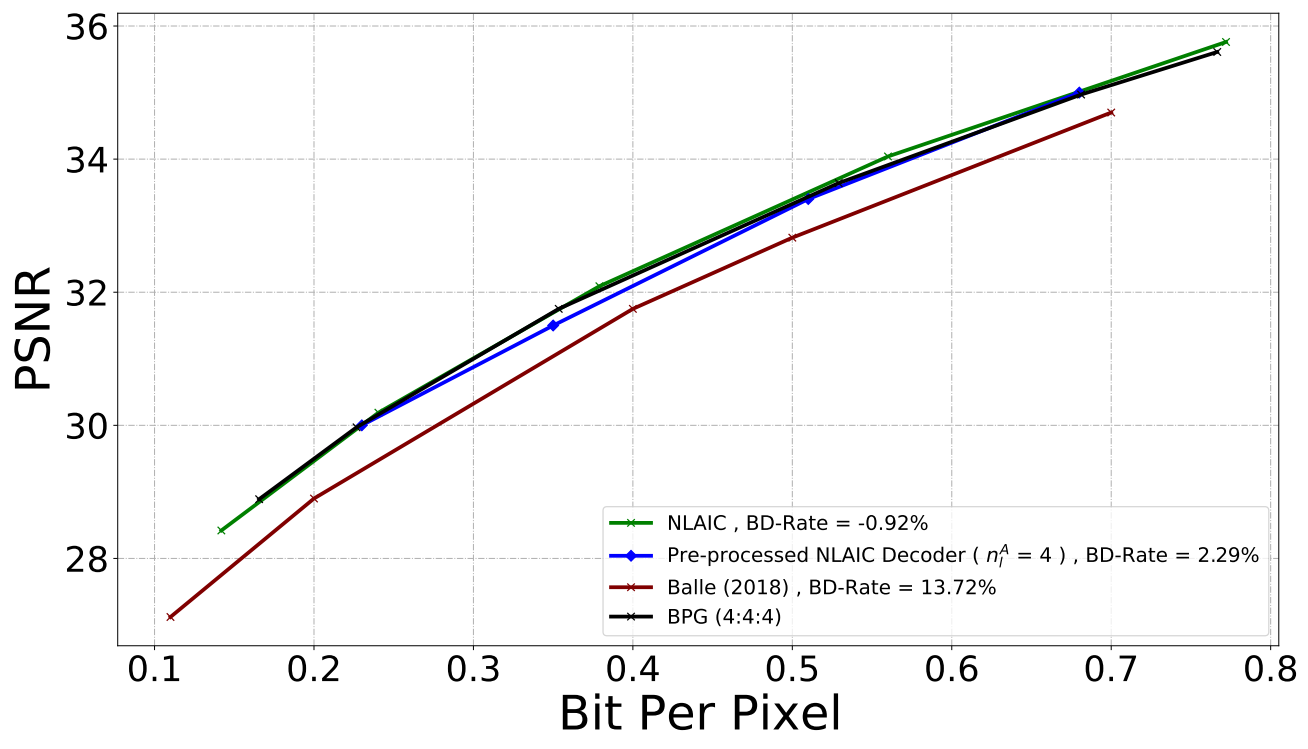
Influence of activations with different bit-width
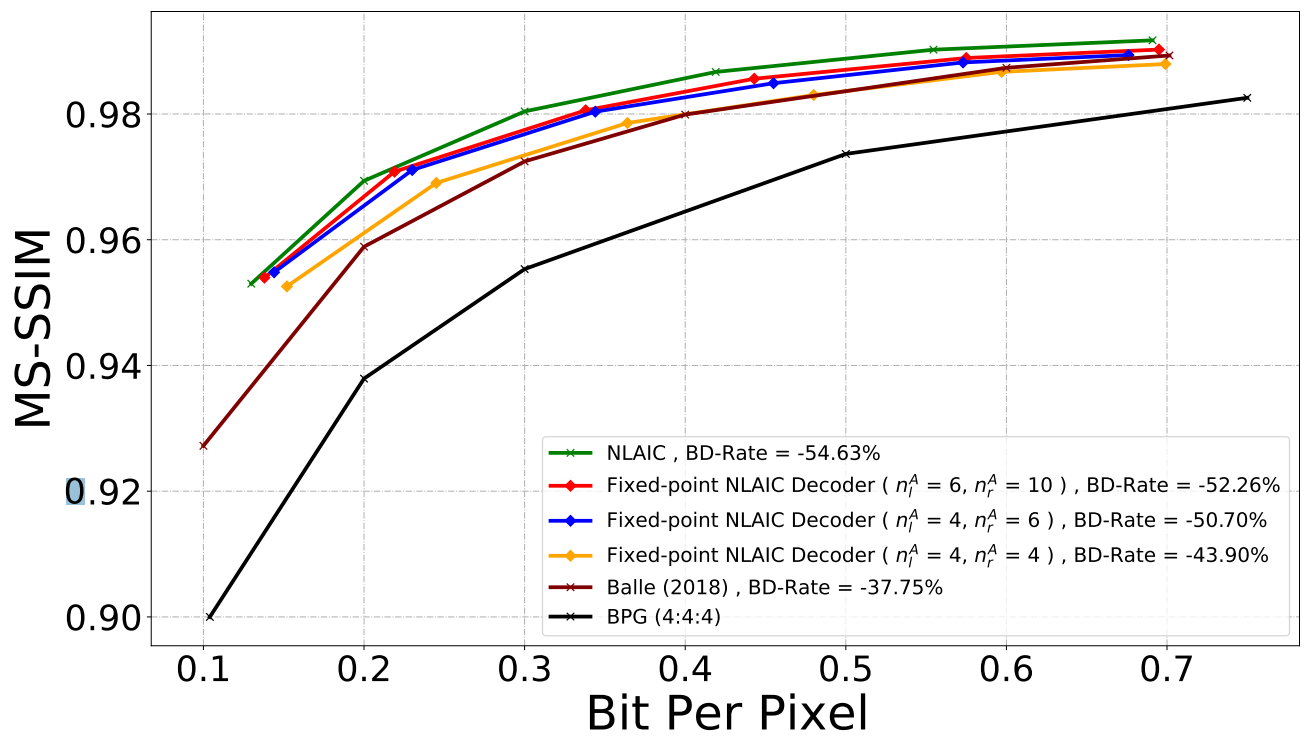
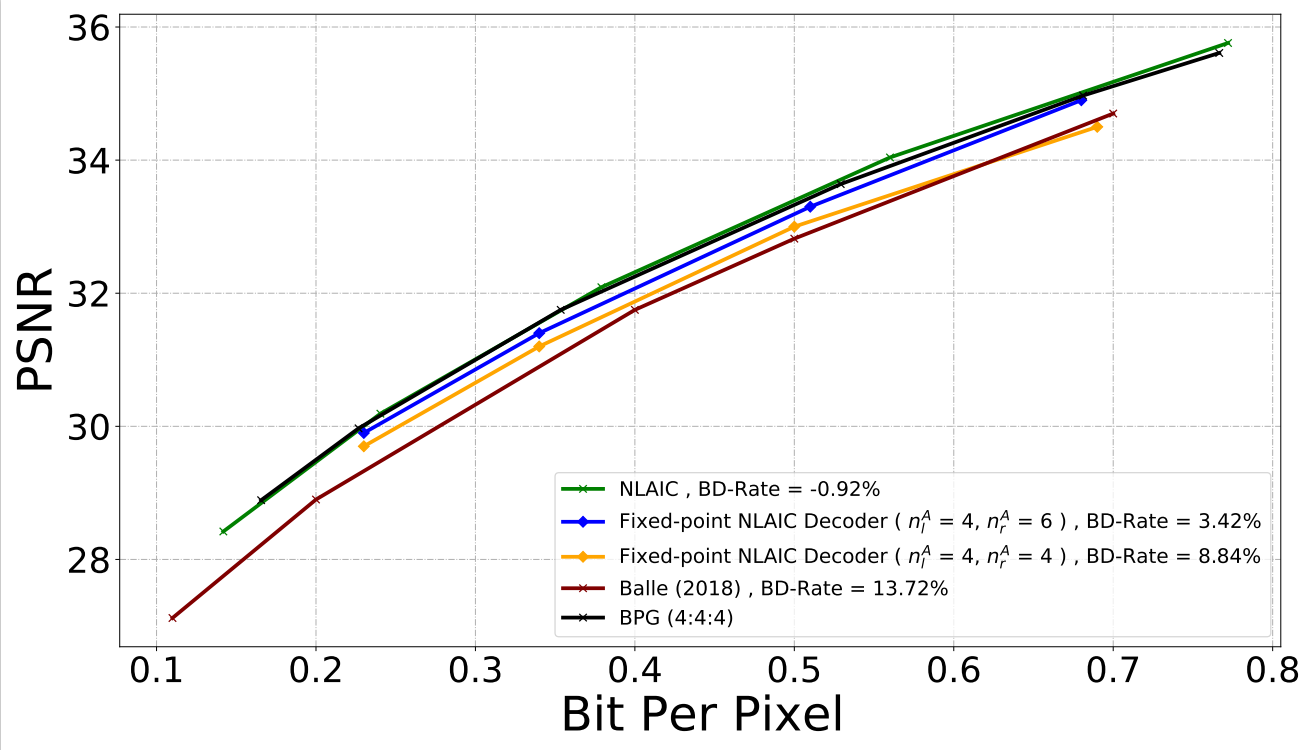
Influence of weights with different bit-width
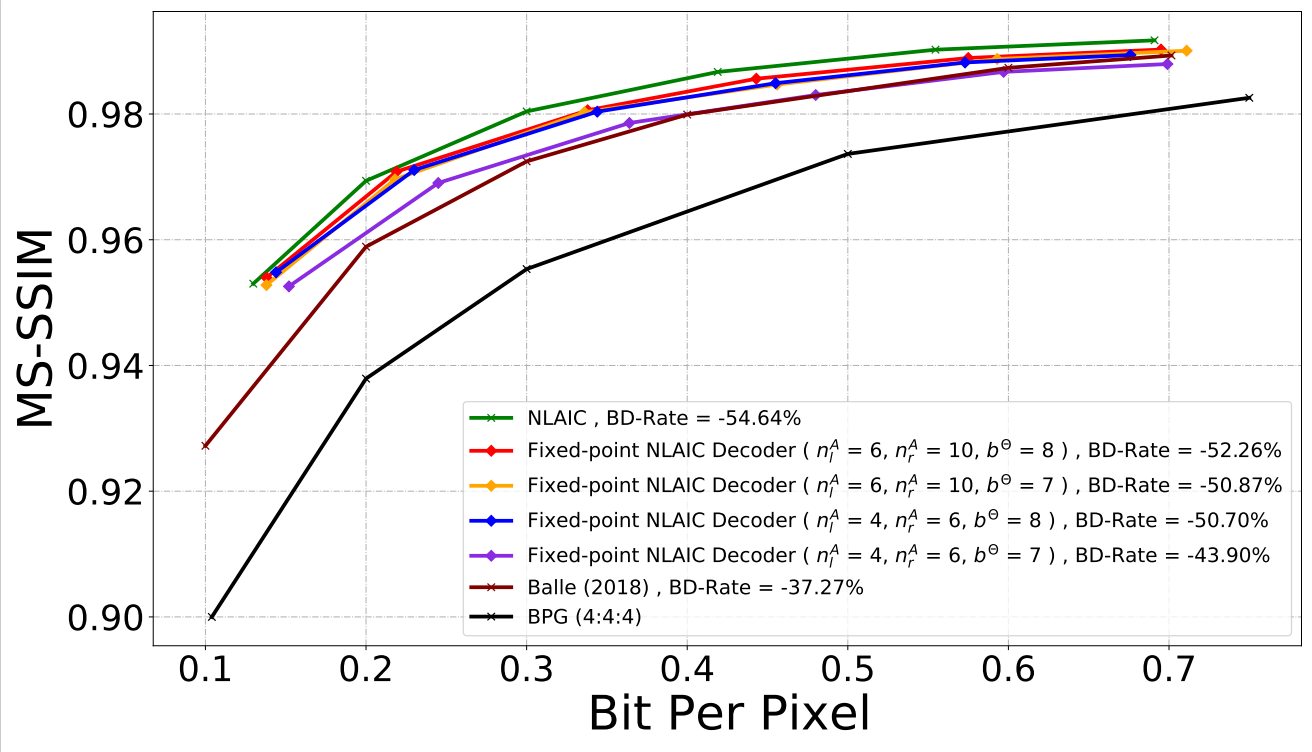
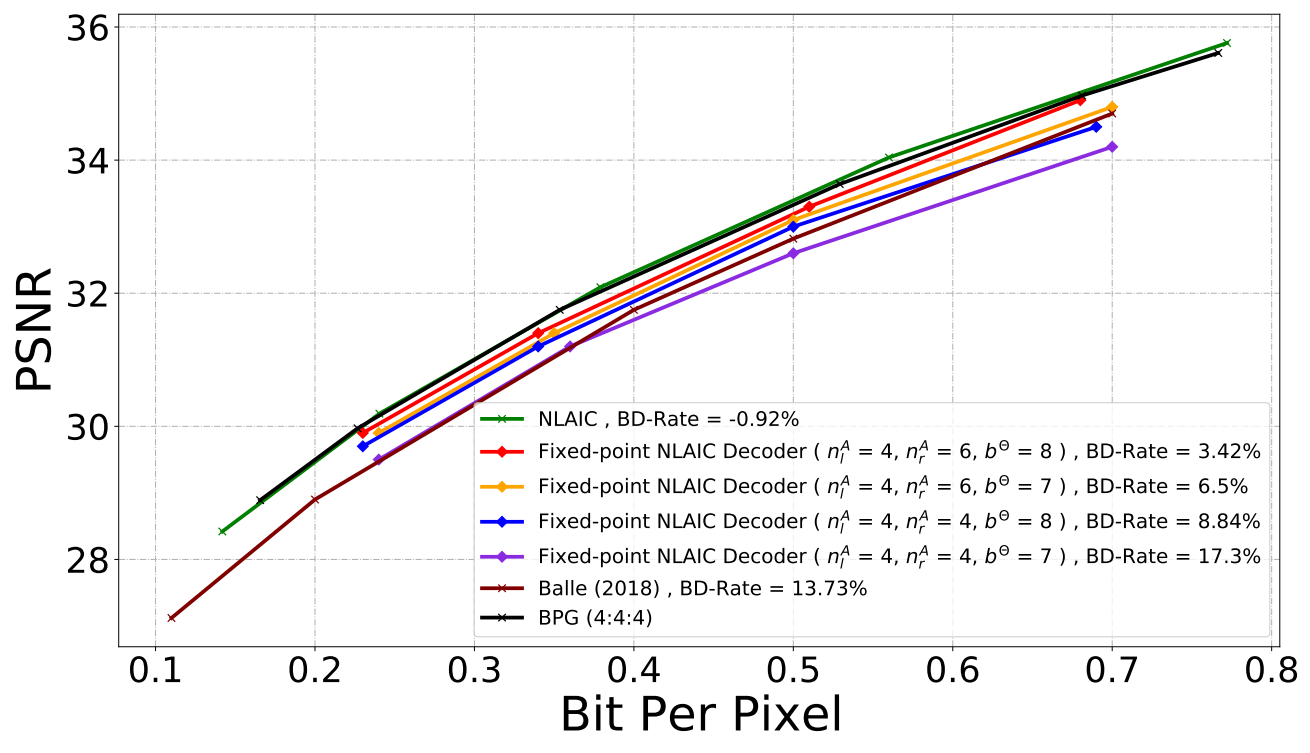
Fully Fixed-point Image Codec